I was working on if it would be better to build surface settlements on the likes of Psyche and Ceres or keep habitats in orbit around the planets. Planetary settlements are nice and stable, but hard to move if you need to get them out of the way of a meteorite strike or enemy attack. Also: when you deplete the resources of a minor planet, a settlement on the surface has to be broken down and launched off the surface. Or abandoned in place.
There is a LOT of math here, and if someone wants to check my work all of the calculations are in the markup for this page
On the other hand, orbital settlements are a giant pain in the ass to move material around to. Yes, most asteroids have tiny escape velocities. However this means that a misplaced bit of thrust can lob that precious ore (or pod full of school kids) out into deep space if the trajectory is just a little bit off.
And in crunching the numbers I discovered some interesting quirks in the rotational properties of the two worlds.
Normally, as objects drop in mass, they spin slower. Earth, as we all know, makes a rotation 360 turn in 23 hours and 56 minutes. A day on Jupiter, which has 320 times Earth's mass, is 9.95 hours long. On Mercury, which has 5% of the mass of Earth, a day lasts 1407 hours.
Psyche and Ceres have quite a bit of spin to them, given their tiny size. Psyche rotates every 4.2 hours. Ceres rotates every 9 hours. That the high spin and the low mass meant gave synchronous equatorial orbit on both worlds some interesting properties.
Synchronous equatorial orbit you may know better as Geostationary Orbit. Essentially, the satellite always sits over the same part of the planet below. And someone on the planet below can always look up and see that satellite in the same chunk of sky. They are great for weather satellites and communication satellites. I was also thinking they would be a great target to aim a mass driver at.
Geosynchronous orbit on Earth happens at a distance of 35,786 km (22,236 miles) above the Earth's equator. A satellite orbing at that distance goes around in 23 hours and 56 minutes. The same speed as the Earth below. A lower orbit makes more passes in a unit time. A higher orbit makes fewer in a unit time. The Moon orbits at mean distance of 385,000 km (239,000 mi). It takes a whole month to go around. The Internation Space Station orbits at a mean distance of 400 kilometres (250 mi). It goes around the world every 93 minutes (about 15.5 orbits per day).
You can compute the radius with this handy equation:
μ is the geocentric gravitational constant of the planetoid.
T is the period (in seconds) of the planet's rotation.
r ends up being the orbital distance, in meters
Space Elevators
In between looking at Mass Drivers I review the math on Space Elevators.
What makes a space elevator work is an interesting quirk of physics that occurs at higher orbits. The centripital force of the orbit starts to exceed the weight of the object due to gravitation. Imagine that our space station on the cable is acting like a bucket of water on a string:
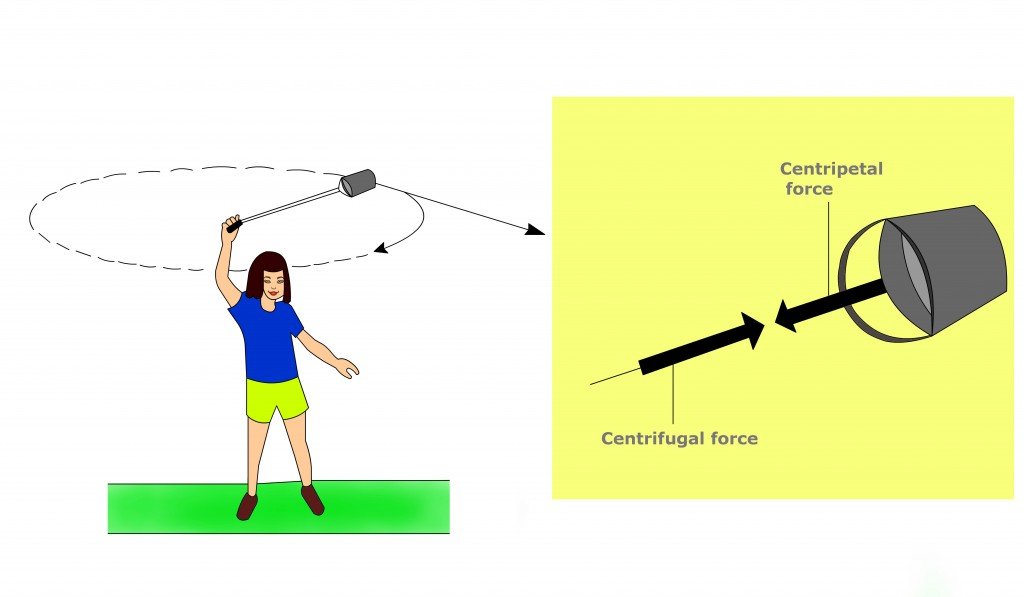
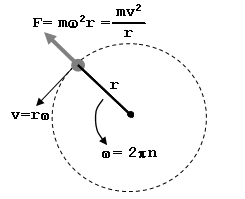
Because these tiny worlds spin as fast as they do, we get that effect at a much shorter distance than, say, the Earth or the Moon. Into the realm where we can implement a plausible Space Elevator. And using steel cable, not some exotic nanomaterial.
We can put all of the chips on the table to solve for at what radius a weight on the end of the cable ceases to put any weight on the cable:
When we solve for when g = 0, and replace a few terms (MG=μ , ω can be converted orbital speed and period (T)) we get:
That's our equation for geostationary orbit. A space station orbiting 16 Psyche just needs to be attached by a cable that is longer than 97.8 km, and have a mass greater than the cable itself to hold the cable in perfect tension.
For a thought experiment, lets make the cable 100km long and the station equal to the mass of the cable itself. There is more than enough nickel/iron in near pure form to fashion them both right from the surface of the planetoid. Let's assume we boost our station (and rolled up cable) to 100km above the planet's surface.
Orbital speed is defined by the equation:
The a is the semi-major axis. As our orbit will be, or all intents and purposes circular, this is the same as our radius.
Now, how thick of a cable are we going to need? Well we kind of have to know how much weight it's going to have to hold. But we actually make giant cables that hold massive weights, and we have been since the 19th century. For suspension bridges.
For our opening bid, lets just hang a cable that is equivilent to one of the main cables on the Golden Gate Bridge. It will hang from a satellite in orbit, straight down to the surface of the planet. For the moment we will ignore the fact the length of the cable in orbit is weighs less than an equivilent length on the planet's surface.
After crunching some numbers both cables on the Golden Gate (and their trappings) have a mass of 22,220,000 kg, and are 2332 meters long. We also know that are .92m in diameter, giving us a cross sectional area of 0.665 m2. This gives is a density of 7164.14 kg/m3. To check our work, the density of solid steel is between: 7750-8670 kg/m3. Wire rope is not solid steel, and the gaps between the wires and galvanic coatings make the cable less dense.
| Body | geostationary radius (planet center) |
geostationary radius (planet surface) |
geostationary speed (meters/second) |
Cable mass (Kg) |
Cable mass (Empire State Buildings) |
| 16 Psyche | 210266 | 97766.2 | 87.4615 | 7.004110e+08 | 2.11526 |
| 1 Ceres | 1191840 | 721844 | 229.2310 | 5.171390e+09 | 15.6178 |
| Luna | 5099120 | 4629120 | 980.767 | 3.316370e+10 | 100.155 |
| Earth | 42164200 | 35786100 | 3074.66 | 2.563760e+11 | 774.265 |
Even for the shortest cable on Psyche, we are talking about a lot of mass of cable. And for my purposes I like to have something to compare it too. So, I chose the mass of Empire State Building (331,122,430 kg).
Ok, so far we have established that for the Asteroid 16 Psyche, we need to lob the mass of 2.1 Empire state buildings worth of cable into an 87.5 m/s orbit. For Earth we would need 368x as much material, boosted to a much faster speed. That is what makes a space elevator for Earth utterly impractical. But for Psyche... it won't be cheap, but we may well be in the realm of what technology could pull off. In fact, this cable weighs less than some of the planetary settlements I have envisioned, and a lot less than some of the spacecraft.
- Length: 100000 m
- Speed: 126.824 m/s
- Total Mass: 9.528310e+08 kg ( 2.88 Empire State Buildings)
- Orbital Kinetic Energy: 1.532560e+13 kg⋅m⋅s−2
- (3662.92 Tons of TNT)
- (2733.3 Saturn V First stages)
- Load: 7.663000e+07 N
- Stress: 1.152000e+08 Pa
- Stretch: 57.61 meters
Ok... so, still a bit of an engineering challenge. The Stretch factor tells you how much the cable is going to elongate under the load of the counterweight. Stress is how much load is on a unit section cable. Repeating the process for Ceres, but with a 730km cable:
- Length: 730000 m
- Speed: 292.913 m/s
- Total Mass: 6.955660e+09 kg ( 21.0 Empire State Buildings)
- Orbital Kinetic Energy: 5.967820e+14 kg⋅m⋅s−2
- (142634 Tons of TNT)
- (106430 Saturn V First stages)
- Stress: 6.147000e+08 Pa
- Stretch: 2243 meters
And for completeness, let's try the Moon with a 4630km cable:
- Length: 4630000 m
- Speed: 1029.25 m/s
- Total Mass: 4.411600e+10 kg ( 133 Empire State Buildings)
- Orbital Kinetic Energy: 4.673510e+16 kg⋅m⋅s−2
- (11169900 Tons of TNT)
- (8335100 Saturn V First stages)
- Stress: 7.589000e+09 Pa
- Stretch: 175700 meters
And finally... Earth. With a 35786km long cable...
- Length: 35786000 m
- Speed: 3337.43 m/s
- Total Mass: 3.409710e+11 kg ( 1030 Empire State Buildings)
- Orbital Kinetic Energy: 3.797990e+18 kg⋅m⋅s−2
- (907741000 Tons of TNT)
- (677360000 Saturn V First stages)
- Stress: 7.971000e+10 Pa
- Stretch: 14280000 meters
Assuming this is science fiction and we have fusion powered rocket engines, and Mass Drivers at our disposal, the energy requirements to get the material in orbit are not all that crazy.
But we have more to wrestle with than energy to orbit. Note that stress column. I picked the cable on the Golden Gate Bridge because we know roughly how much weight it can hold. The strength of wire rope is a very well understood problem in Engineering. The bridge is still standing after nearly a century, so they must have gotten the answer right. Long story short, the strength of a cable increases with the cross sectional area. And you can build up immense cross sectional areas by adding together smaller wires.
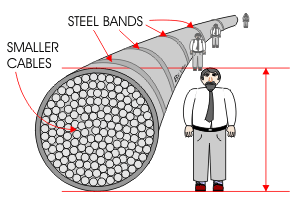

Two cables on the Golden Gate Bridge hold up about 21,772,000 kg of structure. So we can say that each cable is holding up half. But we are concerned with WEIGHT so, we have to remember to multiply mass by Gravity (9.8 m/s^2) to get Newtons: 1.066800e+08 N. The stress on those cables is the load / area. Thus we can guestimate a safe stress to be 1.604200e+08 Pascals.
However raw strength isn't the complete answer. Steel rope (and indeed virtually every structural material) stretches under load. Below the yield strength, steel stretches by a relationship between stress and strain known as the Young's Modulus. Stretch the material to the yield strength. and you will permanently deform the material. The material will continue stretching until the ultimate tensile strength, at which point it will break. For generic structural steel, the Young's Modulus is 2.00e11, the Yield Strength is 2.5e8 Pa, and the Ultimate Tensile Strength is 4.0e+08 Pa.
Our calculation for cable strain on the Golden Gate Bridge (1.604200e+08 Pa) is only a fraction of the yield strength of steel (2.5e8 Pa). This is by design. A bridge needs to handle a lot of strain in addition to its own weight. In fact the operators of the Golden Gate bridge never allow the strain to exceed 40% of the Tensile strength on the cables.
For our Psyche cable we have a stress of 1.152000e+08 Pa. An accountant might say we have 28.2% more rope than would be strictly called for if this cable were on a bridge. What happens if we make the cable 28% smaller?
- Speed: 126.824 m/s
- Cable Area: 0.477 m^2
- Total Mass: 6.834590e+08 kg (2.06 empire state buildings)
- Kinetic Energy: 1.099210e+13 kg⋅m⋅s−2 (2627.39 Tons of TNT) (1960.6 Saturn V First stages)
- Load: 5.496000e+07 N
- Stress: 1.152000e+08 Pa
- Stretch: 57.61 meters
As the size of the cable goes down, so does its mass, and so too does the load needed to keep that mass aloft. The strain remains constant.
If a 28% reduction has such a profound change, what about 98%?
- Speed: 126.824 m/s 0.02
- Cable Area: 0.013 m^2
- Total Mass: 1.862680e+07 kg (0.06 empire state buildings)
- Kinetic Energy: 2.995990e+11 kg⋅m⋅s−2 (71.6059 Tons of TNT) (53.433 Saturn V First stages)
- Load: 1.498000e+06 N
- Stress: 1.152000e+08 Pa
- Stretch: 57.61 meters
Our case for space elevator on Psyche is more or less made. Decide on the mass of your orbiting station, and pretty much size your cable accordingly. The smaller the station, the less cable you need. The less cable you need... the less cable you need. Most of the load is dealing with the weight of the cable.
You will note that for our larger bodies, though, the stress on the rope exceeds not just the Yield strength, but the ultimate tensile strength of Steel. But what if we learned from our little experiment using something with a higher tensile strength? I've picked out a cable that can be purchased, today, from a catalogue. It's 50mm in diameter. It has a breaking strength of 8.281000e+08 Pa. And a mass of 1.3 kg/m. Let's try that out on Ceres, the Moon, and Earth.
Ceres:
- Speed: 292.913 m/s
- Total Mass: 1.898000e+06 kg (0.00 empire state buildings)
- Kinetic Energy: 1.630000e+11 kg⋅m⋅s−2
- Load: 1.115000e+05 N
- Stress: 5.577000e+07 Pa
Luna:
- Speed: 1029.25 m/s
- Total Mass: 1.203800e+07 kg (0.04 empire state buildings)
- Kinetic Energy: 1.275270e+13 kg⋅m⋅s−2
- Stress: 6.886000e+08 Pa
Earth:
- Speed: 3337.43 m/s
- Total Mass: 9.304360e+07 kg (0.28 empire state buildings)
- Kinetic Energy: 1.036360e+15 kg⋅m⋅s−2
- Stress: 7.231000e+09 Pa
Earth... we just can't seem to make it work for Earth. Luna is inside the breaking strength of the cable, but not within any kind of comfortable safety margin. For Ceres, the 50mm cable is well inside the breaking strength.
So in the end, how practical would a space elevator be?
Psyche
The stress and strain needed for a cable would permit massive loads to be moved into orbit using conventional steel. That cable system could scale to practically any size station in orbit.
Ceres
A practical cargo/passenger system could be devised using advanced composite cables. But you aren't moving the likes of ships into orbit with it.
Luna
A cable is possible as a tourist attraction or for moving high-value/low volume cargo. But it's not something that would be cost effective to operate, as the cable will likely fatigue quickly under normal working loads barring it being made of an exotic material.
Earth
Not happening. End of statement.
Images credits:
- https://wikimedia.org/api/rest_v1/media/math/render/svg/1385eed5863f0e40f86905c95cd3d4af7788ce9e
- https://wikimedia.org/api/rest_v1/media/math/render/svg/07005f1d6ce59ad5df80225ee26642603650be0e
- https://wikimedia.org/api/rest_v1/media/math/render/svg/c597ae5584d3dd6749cf0c49908afa9df45e9c5a
- https://www.scienceabc.com/wp-content/uploads/2018/08/centripital-force.jpg
- https://www.engineersedge.com/physics/centrifugal-force.gif
- https://wikimedia.org/api/rest_v1/media/math/render/svg/c86493d99fd1b940ca6e1ed1fdc0157c86580263
- https://technologystudent.com/images6/susp1.gif
- https://c8.alamy.com/comp/F7278F/multi-colored-strands-of-a-bridge-suspension-cable-from-the-new-span-F7278F.jpg
- https://www.inside-guide-to-san-francisco-tourism.com/images/golden-gate-bridge-cable-cross-section.jpg
- http://www.hampidjan.com.au/images/dynice-warp-winch-diagram.jpg